Welcome … — Physics-based Deep Learning
www.physicsbaseddeeplearning.org
Overview
2.1 Motivation
Replacing traditional simulations?
딥러닝은 이미 많은 분야에서 뛰어난 성과를 보였지만, 이 기술이 최대의 잠재력을 발휘하기 위해서는 물리 모델의 도메인 지식이 필요하다. 전통적인 수치 모델링 방법은 정확하고 신뢰할 수 있는 결과를 제공하는 반면, 딥러닝은 모델링을 통해 얻은 데이터로부터 더 심층적인 통찰력을 추출할 수 있다. 이 책은 딥러닝을 적용할 때 전통적인 수치 수학 방법을 활용하는 것의 중요성을 강조하며, 두 결합이 다음 세대의 시뮬레이션 시스템 발전에 핵심적일 것임을 주장한다.
Reconciling DL and simulations
본 책은 수치 시뮬레이션과 딥러닝 기술을 결합하여 사용하는 것을 목표로 한다. 중점은 데이터 중심의 관점과 물리 시뮬레이션을 조화롭게 통합하는 데 있으며, 딥러닝을 활용해 PDE 문제를 해결하고 물리학 지식을 적용하는 방법을 탐구한다.
※ PDE(Partial Differential Equations) : 부분 미분 방정식, 유체의 흐름, 열 전달, 전자기장, 음파 전파와 같은 다양한 현상을 모델링하는 데 사용
2.2 Categorization
물리 기반 딥러닝 분야는 순방향 시뮬레이션과 역문제 해결을 목표로 하며, 딥러닝 기술과 도메인 지식의 통합에 초점을 맞춘다. 이는 주로 부분 미분 방정식을 통한 모델 방정식을 사용하고, 접근법은 크게 세 가지로 분류된다.

1. Supervised
- 데이터는 물리 시스템(실제 또는 시뮬레이션된)에 의해 생성된다.
- 추가적인 상호작용은 존재하지 않는 클래식 머신 러닝 접근법을 의미한다.
2. Loss-terms
- 물리 동역학(또는 그 일부)은 손실 함수에 인코딩 되며, 미분 가능한 연산의 형태로 나타낸다.
- 학습 과정은 반복적으로 손실을 평가할 수 있으며, 보통 PDE 기반 공식으로부터 gradient를 받는다.
- 이러한 소프트 제약은 때때로 "물리 정보 훈련”이라고도 불린다.
3. Interleaved
- 완전한 물리 시뮬레이션은 딥 뉴럴 네트워크의 출력과 교차 배치되어 결합된다.
- 물리 시스템과 학습 과정 간의 가장 긴밀한 결합을 나타낸다.
- 미분 가능한 물리 접근법은 특히 시간적 진화에 있어 중요한데, 이를 통해 동역학의 미래 행동에 대한 추정치를 제공한다.
위 방법들은 딥러닝과 수치 시뮬레이션을 긴밀하게 통합하여, 순방향 문제나 역문제를 효과적으로 해결하는 새로운 방식을 제공한다.
2.4 Implementations
파이토치(pytorch)와 텐서플로(tensorflow)와 같은 인기 있는 딥러닝 API를 사용할 것이며, 미분 가능한 시뮬레이션 프레임워크인 𝜑Flow(phiflow)에 대해서도 소개한다. 이러한 예제들을 살펴본 후에는 현재 API에서 사용할 수 있는 것들에 대한 좋은 개요를 가질 수 있어, 새로운 작업에 가장 적합한 API를 선택적으로 사용 수 있을 것이다.
2.5 Models and Equations
Deep learning and neural networks
본 책은 물리 모델과의 연결에 초점을 맞추고 있으며, 딥러닝에 대한 훌륭한 소개가 많이 있다. 간단한 예제로, 딥러닝의 목표는 이상적인 함수 f∗(x) [수식 (1) 함수]를 근사하는 것이다.

- y∗ : ground truth
- f∗(x)는 → f(x;θ)로 근사되는 것이 목표
- θ : 신경망의 가중치(파라미터)
- 오차 함수 e(y,y∗) : 통해 실제 출력 y 와 참값 y∗ 사이의 차이(오류) 계산 즉, e를 최소화
- 가장 간단한 경우에는 L2 error을 사용하여 계산 수 있으며, 아래와 같이 표현

- 신경망의 가중치 θ 를 찾는것을 목표로하며 선택한 확률적 경사 하강법(SGD) 또는 Adam을 사용하여 최적화(즉, 훈련) 진행
- 자동 미분은 손실 함수 L의 가중치에 대해 계산 gradient를 계산하는데 사용
Partial differential equations as physical models
PDE는 자연 현상, 공학 문제 등을 수학적으로 모델링할 때 주로 사용되는 방정식이다. 이러한 방정식의 해는 특정 공간 영역과 시간에 따라 변화하는 물리적 상태를 설명해주며, 딥러닝을 이용한 수치 시뮬레이션에서는 이러한 방정식의 해를 효율적으로 찾는 것을 목표로 한다.
부분 미분 방정식(PDE)
- P∗로 표기된 연속적인 PDE는 우리가 해결하고자 하는 방정식을 의미
- 이 방정식들은 PDE의 공간 영역 Ω⊂R^d, d∈{1,2,3}차원에서의 해를 구하는 것이 목표
시간 진화(Time Evolution)
- 문제는 종종 시간에 따라 변화하는 상태를 모델링하므로, 유한한 시간 간격 t∈R^+에 대한 변화를 고려
영역(Field)
- 관련 필드(즉, 물리적 상태를 나타내는 수학적 표현)는 벡터 필드나 스칼라 필드일 수 있음
- 벡터 필드 예시로는 u가 있으며, 이는 d차원 공간과 시간에 대한 함수이다. ex) u : Rd × R+ → Rd
- 스칼라 필드 예시로는 p가 있으며, 이는 각 지점과 시간에 대한 단일 값(스칼라 값)을 가짐 ex) p : Rd × R+ → R
표기법(Notation)
- 벡터의 각 구성요소는 보통 x,y,z와 같은 첨자를 사용해 표기됨
- 예를 들어, 3차원의 경우 벡터 v는 vx, vy, vz로 구성된 벡터 v=(vx, vy, vz)T
- 위치는 공간 영역 Ω 내의 특정 점을 나타내는 x로 표기
부분 미분 방정식(PDE) 𝒫에 대한 고유한 해를 얻기 위해, 우리는 초기 조건을 t=0에서 설정하고, 공간 영역 Ω의 경계에 대한 경계 조건을 제공해야 한다. 𝒫는 연속적인 공식으로, 일반적으로 그 연속성과 첫 번째 및 두 번째 미분의 존재를 가정한다. 수치 방법을 통해 𝒫* 같은 연속적인 함수의 근사치를 이산화하여 얻으며, 이 과정에서 발생하는 이산화 오류를 최소화 한다. 이 오류는 해석적 해와의 차이로 측정되며, PDE의 이산 시뮬레이션에서는 절단 오류 O(∆xk)로 표현된다. 여기서 ∆x는 공간 이산화의 단계 크기이고, 시간적 이산화는 시간 단계 ∆t를 통해 이루어진다.
※ 초기조건 : ex) t = 0 에서의 온도 분포, 물질의 농도 등
※ 경계조건 : ex) 온도, 압력, 또는 벽에 대한 유체의 흐름 조건 등
Notation and abbreviations (표기법 및 약어)
이산화된 부분 미분 방정식(PDE) 𝒫을 해결하기 위해 크기가 ∆𝑡인 단계를 수행하며, 해는 함수 u와 그 공간 미분, 예를 들어 u(x,t+Δt) = P(ux, uxx, … , uxx…x), 로 표현된다. 여기서 ux는 공간 미분 ∂u(x,t) / ∂x를 나타낸다. 모든 PDE에 대해, 실제 세계 양으로 재조정할 수 있는 적절한 스케일링 인자를 사용하여 비차원화된 매개변수화를 가정한다.
※ P(ux, uxx, … , uxx…x) : 공간 미분을 의미
Some example PDEs
Burgers Equation(버거스 방정식)
잘 연구된 PDE를 대표하며, (나비에-스톡스와는 달리) 질량 보존과 같은 추가적인 제약 조건을 포함하지 않아서, 흥미로운 충격 형성을 이끌어낸다. 이 방정식은 이동/수송을 나타내는 이류 항과 열역학 제2법칙에 의한 소산을 나타내는 확산 항을 포함한. 2차원에서는 다음과 같이 주어진다.
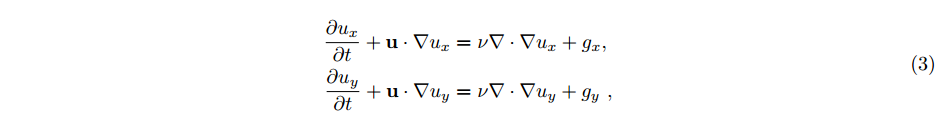
- u : 유체의 속도 필드
- ∂u/∂t : 시간에 따른 유체의 속도 변화
- ∇u : u의 gradient(공간적 미분)
- u⋅∇ u : 비선형 항*,* 유체의 속도 필드 내에서 유체의 속도가 공간적으로 어떻게 변하는지 나타냄
- ν **: 확산 상수
- ν∇∙∇u : 점섬 항, 유체의 점성으로 인해 발생하는 속도의 확산을 의미
- g : 외부 힘
1차원에서의 버거스 방정식은 더 단순한 변형으로, 단일 1차원 속도 성분을 u = u_x로 표기하며 다음과 같이 주어진다.
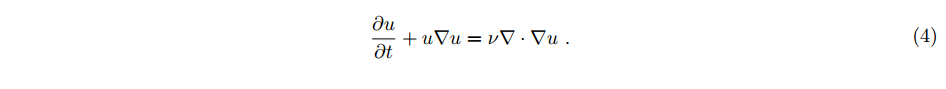
Navier-Stokes(나비에-스트로크 방정식)
나비에-스토크스 방정식은 유체 모델에 있어서 복잡성 측면에서 좋은 다음 단계를 제공한다. 버거스 방정식과 유사한 운동량 보존 방정식뿐만 아니라, 질량 보존 방정식을 포함하는 것이 특징이다. 이는 충격파 형성을 방지하지만, 발산이 없는 운동에 대한 엄격한 제약 조건의 형태로 수치 방법에 새로운 도전을 제시한다.
2차원에서 외부 힘이 없는 나비에-스토크스 방정식은 다음과 같이 쓸 수 있다.
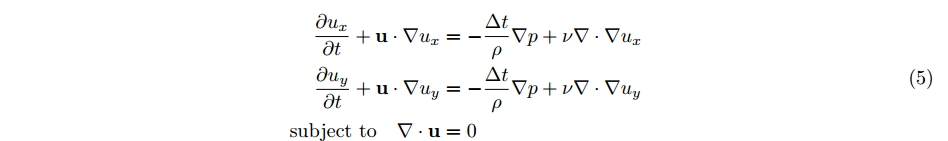
- (∂u_x)/∂t, (∂u_y)/∂t : 각각 x, y 방향 속도의 시간에 따른 변화율
- u∇u_x, u∇u_y : 각각 x, y 방향 유체 속도의 공간적 변화를 의미
- -∆t/ρ ∇p : 압력 gradient의 영향을 의미, ρ는 유체의 밀도, ∇p는 압력의 공간적 변화
- ν∇∙∇u_x, ν∇∙∇u_y : 점성에 의한 x, y 방향 속도의 확산을 의미
- ∇∙u=0 : 유체가 압축 불가능하다는 것을 의미하는 무발산 조건, 유체의 어느 부분도 부피가 변하지 않는다는 의미
Boussinesq 근사를 사용하여 온도에 따라 변화하는 밀도를 고려한 Navier-Stokes 방정식의 변형은 다음과 같은 일련의 방정식을 통해 표현할 수 있다. 이때, maker field v는 높은 온도 영역을 의미하며, 유체 내에서 온도 변화를 표현한다.
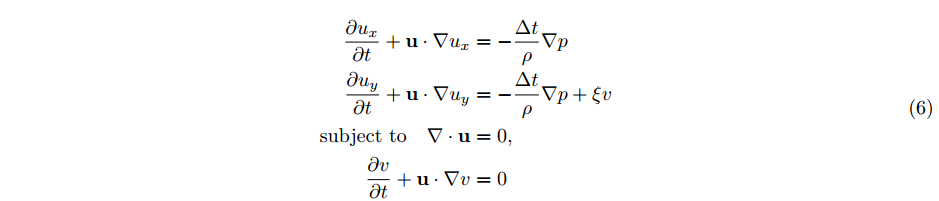
- ξv : 온도가 높은 영역에서 유체가 받는 부력을 의미, ξ는 부력의 강도를 나타내는 상수 해당 추가항은 뜨거운 유체가 상승(y축)하는 현상을 모델링
- ∂v/∂t+u∙∇v=0 : 유체 내부 온도 분포가 시간에 따라 어떻게 변화하는지, 유체의 흐름에 따른 온도의 대류
그리고 마지막으로, 3D Navier-Stokes 모델은 다음과 같은 일련의 방정식을 제공한다.
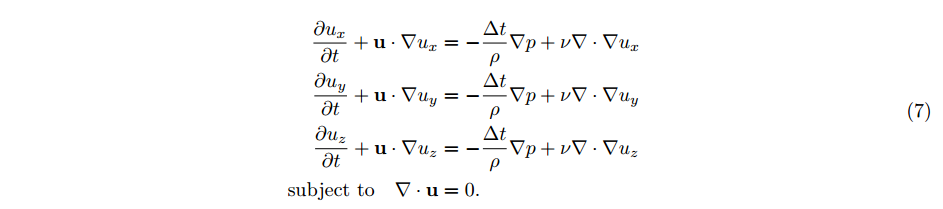
- ∇ · 𝑢 = 0으로 제한
2.6 Simple Forward Simulation of Burgers Equation with phiflow

Model
물리 모델로는 버거스 방정식을 사용한다. 이 방정식은 매우 단순하지만 비선형이며 비자명한 모델 방정식으로, 흥미로운 충격파 형성을 일으킬 수 있다. 버거스 방정식의 1차원 버전(방정식 (4)에서)은 다음과 같다.
𝜕𝑡 + 𝑢∇𝑢 = 𝜈∇ · ∇𝑢 (4)
Importing and loading phiflow
from phi.flow import *
from phi import __version__
N = 128 # 그리드 셀 수
DX = 2./N # Dx = 각 셀의 공간적 크기
STEPS = 32 # 시간 스텝
DT = 1./STEPS # 각 시간 스텝의 길이
NU = 0.01/(N*np.pi) # 유체의 점섬
# N개의 이산화 점 생성
# 도메인의 양 끝에 있는 셀의 중앙은 각각 −1+DX/2 및 1−DX/2에 위치하기 때문에 다음과 같은 구간 설정
print(np.linspace(-1+DX/2, 1-DX/2, N), end="\\n\\n")
# initialization of velocities, cell centers of a CenteredGrid have DX/2 offsets for linspace()
# -1 ~ 1 사이의 x좌표를 생성하고, 각 x에 대해 초기 속도 값 계
INITIAL_NUMPY = np.asarray( [-np.sin(np.pi * x) for x in np.linspace(-1+DX/2,1-DX/2,N)] ) # 1D
INITIAL = math.tensor(INITIAL_NUMPY, spatial('x') ) # convert to phiflow tensor
print(INITIAL_NUMPY[1] - INITIAL_NUMPY[0])
Result
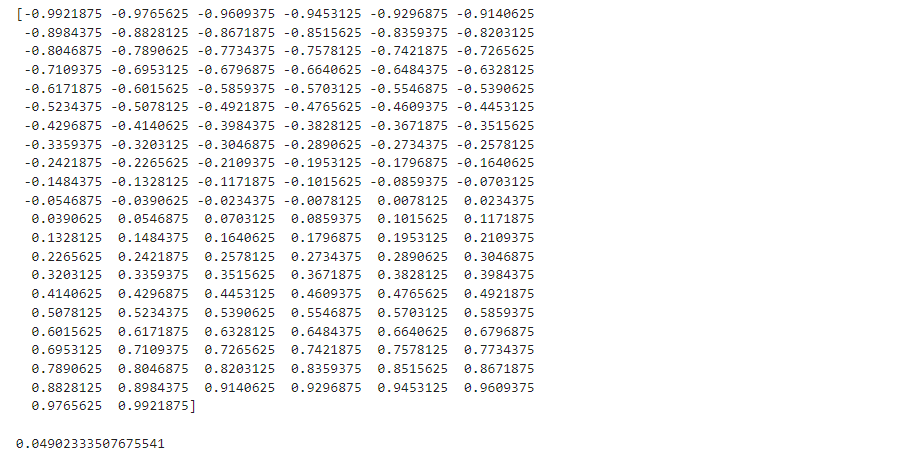
Running the simulation
velocity = CenteredGrid(INITIAL, extrapolation.PERIODIC, x=N, bounds=Box[-1:1])
vt = advect.semi_lagrangian(velocity, velocity, DT)
#velocity = CenteredGrid(lambda x: -math.sin(np.pi * x), extrapolation.PERIODIC, x=N, bounds=Box[-˓→1:1])
**#velocity = CenteredGrid(Noise(), extrapolation.PERIODIC, x=N, bounds=Box[-1:1]) # random init**
print("Velocity tensor shape: " + format( velocity.shape )) # == velocity.values.shape
print("Velocity tensor type: " + format( type(velocity.values) ))
print("Velocity tensor entries 10 to 14: " + format( velocity.values.numpy('x')[10:15] ))
velocities = [velocity]
age = 0.
for i in range(STEPS):
v1 = diffuse.explicit(velocities[-1], NU, DT) # 현재 속도 필드에 대한 확산 단계 계산
v2 = advect.semi_lagrangian(v1, v1, DT) # v1을 자기 자신에 의해 이동시킴
age += DT
velocities.append(v2)
print("New velocity content at t={} : {} ".format( age, velocities[-1].values.numpy('x,vector')[0:5] ))
- velocity = CenteredGrid(INITIAL, extrapolation.PERIODIC, x=N, bounds=Box[-1:1])
- 초기 상태 텐서를 사용하여 중심 정렬된 1D 속도 그리드를 생성
- extrapolation.PERIODIC을 사용하여 -1~1 사이의 영역(bounds)에 N개의 셀을 가짐
- advect.semi_lagrangian(세미 라그랑주) 유체의 이동을 계산하기 위한 방법 / Δt 동안 어디로 이동했는지를 계산
- vt = advect.semi_lagrangian(velocity, velocity, DT)
- 첫 번째 velocity : 현재 시점에서의 유체의 속도 필드
- 두 번째 velocity : 속도 필드 자체를 통해 어떻게 유체가 이동하는지를 나타내는 '운반 벡터'(advection vector), 여기서는 동일한 속도 필드를 사용
- DT : 시간 간격으로, 한 시간 스텝의 크기를 나타냄
Result

Visualization
STEPS = 0, 10, 20, 32
# get "velocity.values" from each phiflow state with a channel dimensions, i.e. "vector"
vels = [v.values.numpy('x,vector') for v in velocities] # gives a list of 2D arrays
import pylab
fig = pylab.figure().gca()
fig.plot(np.linspace(-1,1,len(vels[ 0].flatten())), vels[ 0].flatten(), lw=2, color='blue', label="t=0")
fig.plot(np.linspace(-1,1,len(vels[10].flatten())), vels[10].flatten(), lw=2, color='green', label="t=0.3125")
fig.plot(np.linspace(-1,1,len(vels[20].flatten())), vels[20].flatten(), lw=2, color='cyan', label="t=0.625")
fig.plot(np.linspace(-1,1,len(vels[32].flatten())), vels[32].flatten(), lw=2, color='purple',label="t=1")
pylab.xlabel('x'); pylab.ylabel('u'); pylab.legend()
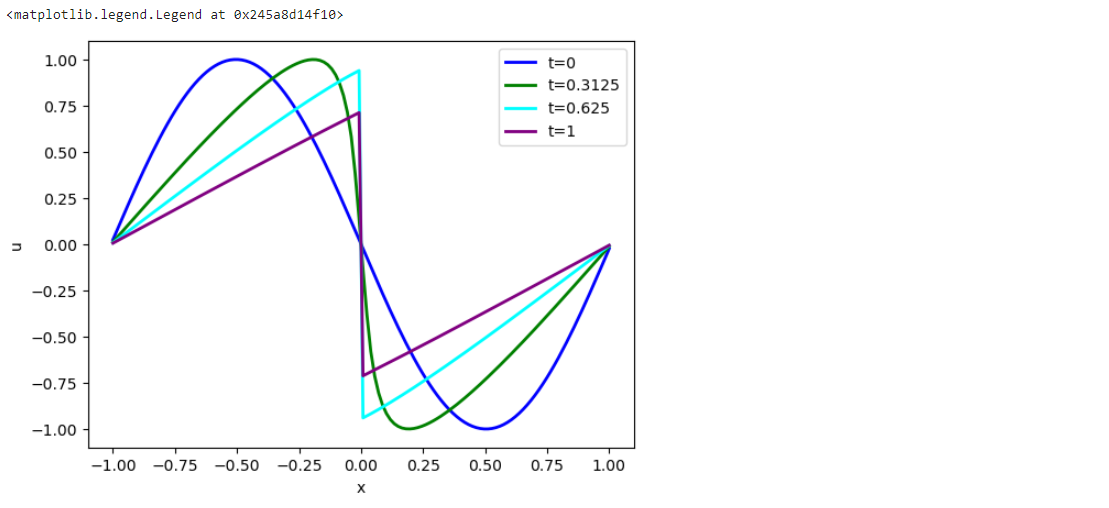
초기 속도 봉우리가 충돌하여 도메인 중앙에 충격파가 형성됨
STEPS = 0 ~ 32
# get "velocity.values" from each phiflow state with a channel dimensions, i.e. "vector"
vels = [v.values.numpy('x,vector') for v in velocities] # gives a list of 2D arrays
import pylab
fig = pylab.figure().gca()
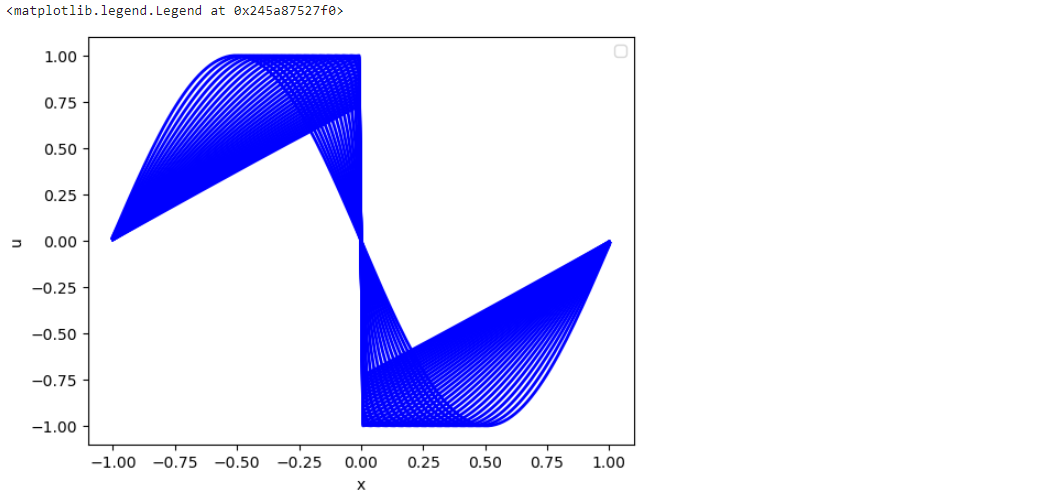
for i in range(STEPS):
fig.plot(np.linspace(-1,1,len(vels[ i].flatten())), vels[ i].flatten(), lw=2, color='blue')
pylab.xlabel('x'); pylab.ylabel('u'); pylab.legend()
Show state
def show_state(a, title):
# we only have 33 time steps, blow up by a factor of 2^4 to make it easier to see
# (could also be done with more evaluations of network)
a=np.expand_dims(a, axis=2)
for i in range(4):
a = np.concatenate( [a,a] , axis=2)
a = np.reshape( a, [a.shape[0],a.shape[1]*a.shape[2]] )
#print("Resulting image size" +format(a.shape))
fig, axes = pylab.subplots(1, 1, figsize=(16, 5))
im = axes.imshow(a, origin='upper', cmap='inferno')
pylab.colorbar(im) ; pylab.xlabel('time'); pylab.ylabel('x'); pylab.title(title)
vels_img = np.asarray( np.concatenate(vels, axis=-1), dtype=np.float32 )
# save for comparison with reconstructions later on
import os; os.makedirs("./temp",exist_ok=True)
np.savez_compressed("./temp/burgers-groundtruth-solution.npz", np.reshape(vels_img,[N,STEPS+1])) # remove batch & channel dimension
show_state(vels_img, "Velocity")
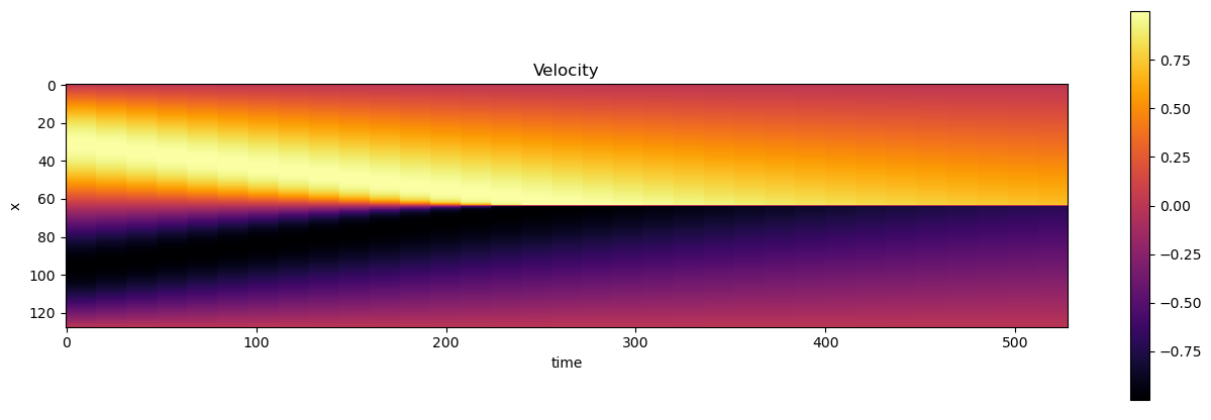
- 모든 시간 단계에 따른 변화를 2D 이미지로 시각화
- 1차원 도메인은 y축을 따라 표시되며, x축의 각 점은 하나의 시간 단계를 의미
2.7 Navier-Stokes Forward Simulation
다음은 Navier-Stokes 방정식에 기반한 유체 시뮬레이션이다. Navier-Stokes 방정식(비압축성 형태에서)은 추가적인 압력 필드 𝑝과, 식 (6)에서 소개된 질량 보존의 제약을 도입한다. 또한, 여기에서 𝑑로 표시된 마커 필드를 흐름과 함께 움직인다. 이는 높은 온도의 영역을 나타내며, 부력 계수 𝜉를 통해 힘을 발휘한다.
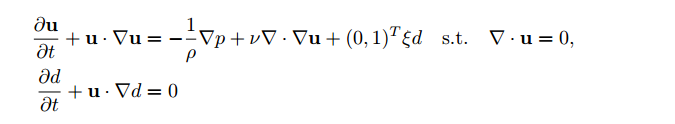
- Boussinesq 근사법을 통한 간단한 부력 모델(항 (0, 1)𝑇 𝜉𝑑)을 사용
- 밀도의 변화를 𝜌을 명시적으로 계산하지 않고 모델링
- 부력이 y 방향으로 작용한다고 가정하여 벡터 (0, 1)𝑇로 표현
- 속도에 대한 Dirichlet 경계 조건 u = 0과 압력에 대한 Neumann 경계 조건 𝜕𝑝/𝜕𝑥 = 0을 가진 닫힌 도메인 Ω에서 100 × 80 단위의 물리적 크기로 이 PDE를 설정
Setting up the simulation
DT = 1.5
NU = 0.01
INFLOW = CenteredGrid(Sphere(center=(30,15), radius=10), extrapolation.BOUNDARY, x=32, y=40, bounds=Box[0:80, 0:100]) * 0.2
smoke = CenteredGrid(0, extrapolation.BOUNDARY, x=32, y=40, bounds=Box[0:80, 0:100]) # sampled at cell centers
velocity = StaggeredGrid(0, extrapolation.ZERO, x=32, y=40, bounds=Box[0:80, 0:100]) # sampled in staggered form at face centers
def step(velocity, smoke, pressure, dt=1.0, buoyancy_factor=1.0):
smoke = advect.semi_lagrangian(smoke, velocity, dt) + INFLOW # 연기 필드를 유체의 속도 필드에 따라 이동시킴
buoyancy_force = (smoke * (0, buoyancy_factor)).at(velocity) # 부력 힘 계산
velocity = advect.semi_lagrangian(velocity, velocity, dt) + dt * buoyancy_force # 속도 이동 및 부력 추가
velocity = diffuse.explicit(velocity, NU, dt) # 유체의 점섬으로 인한 속도의 확산을 계산
velocity, pressure = fluid.make_incompressible(velocity) # 비압축성을 만족하도록 속도 필드에서 발산 제거
return velocity, smoke, pressure
velocity, smoke, pressure = step(velocity, smoke, None, dt=DT)
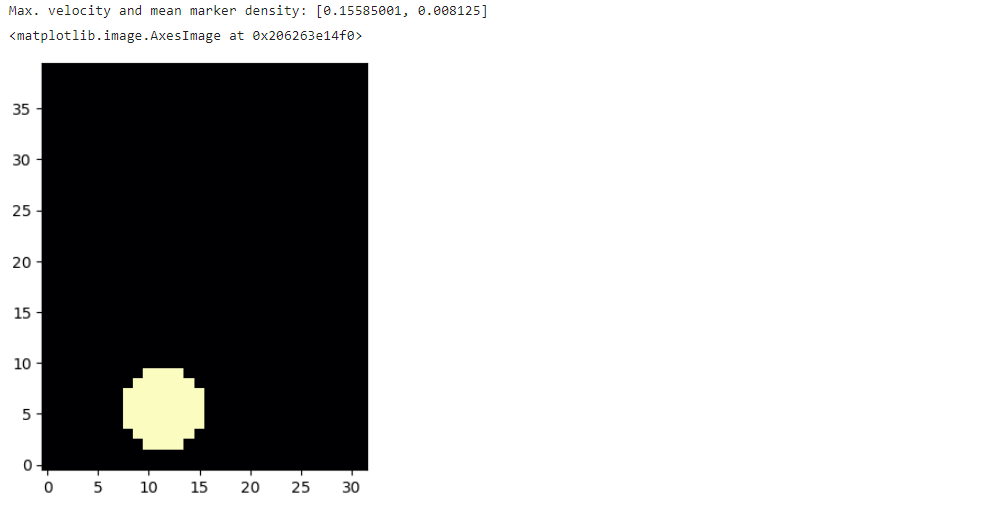
print("Max. velocity and mean marker density: " + format( [ math.max(velocity.values) , math.mean(smoke.values) ] ))
pylab.imshow(np.asarray(smoke.values.numpy('y,x')), origin='lower', cmap='magma')
- smoke = CenteredGrid(0, extrapolation.BOUNDARY, x=32, y=40, bounds=Box[0:80, 0:100])
- smoke :연기 농도를 나타내는 그리드
- CenteredGrid : 각 셀의 중심에서 값이 sampling되는 방식 (마커 필드 d를 의미)
- 연기가 없는 상태(초기값 0)로 초기화, 연기는 시뮬레이션 과정에서 유입영역(INFLOW)를 통해 유입
- extrapolation.BOUNDARY : 그리드의 경계에 대한 처리 방식을 지정, 해당 방식은 경계에서 값이 고정됨
- velocity = StaggeredGrid(0, extrapolation.ZERO, x=32, y=40, bounds=Box[0:80, 0:100])
- velocity : 유체의 속도를 나타내는 그리드
- StaggeredGrid : 각 셀의 표면 중심에서 속도가 sampling되는 방식 (x, y방향 속도를 각각 나타내는 2개의 CenteredGrid 존재)
- 0으로 초기화
- extrapolation.ZERO : 그리드의 경계를 넘어선 위치에서 속도 값이 0이 됨
Result
Datatypes and dimensions
print(f"Smoke: { smoke.shape} ")
print(f"Velocity: { velocity.shape} ")
print(f"Inflow: { INFLOW.shape} , spatial only: { INFLOW.shape.spatial} ")
print(f"Shape content: { velocity.shape.sizes} ")
print(f"Vector dimension: { velocity.shape.get_size('vector')} ")
print("Statistics of the different simulation grids:")
print(smoke.values)
print(velocity.values)
# in contrast to a simple tensor:
test_tensor = math.tensor(numpy.zeros([2, 5, 3]), spatial('x,y'), channel('vector'))
print("Reordered test tensor shape: " + format(test_tensor.numpy('vector,y,x').shape) )
#print(test_tensor.values.numpy('y,x')) # error! tensors don't return their content via ".values"

phiflow에서는 공간적 차원(spatial)을 ‘S’, 벡터 차원(vector)를 ‘V’로 표시
Time evolution
for time_step in range(10):
velocity, smoke, pressure = step(velocity, smoke, pressure, dt=DT)
print('Computed frame {} , max velocity {} '.format(time_step , np.asarray(math.max(velocity.values)) ))
pylab.imshow(smoke.values.numpy('y,x'), origin='lower', cmap='magma')
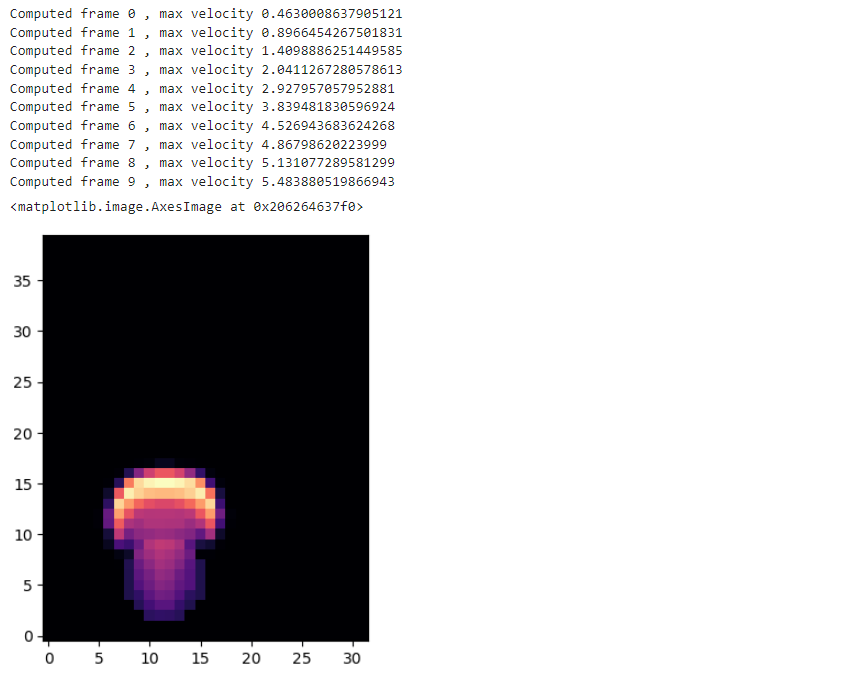
t = 0, 5, 10 , 15, 20
steps = [[ smoke.values, velocity.values.vector[0], velocity.values.vector[1] ]]
for time_step in range(20):
if time_step<3 or time_step%10==0:
print('Computing time step %d ' % time_step)
velocity, smoke, pressure = step(velocity, smoke, pressure, dt=DT)
if time_step%5==0:
steps.append( [smoke.values, velocity.values.vector[0], velocity.values.vector[1]] )
fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
axes[i].imshow(steps[i][0].numpy('y,x'), origin='lower', cmap='magma')
axes[i].set_title(f"d at t={ i*5} ")
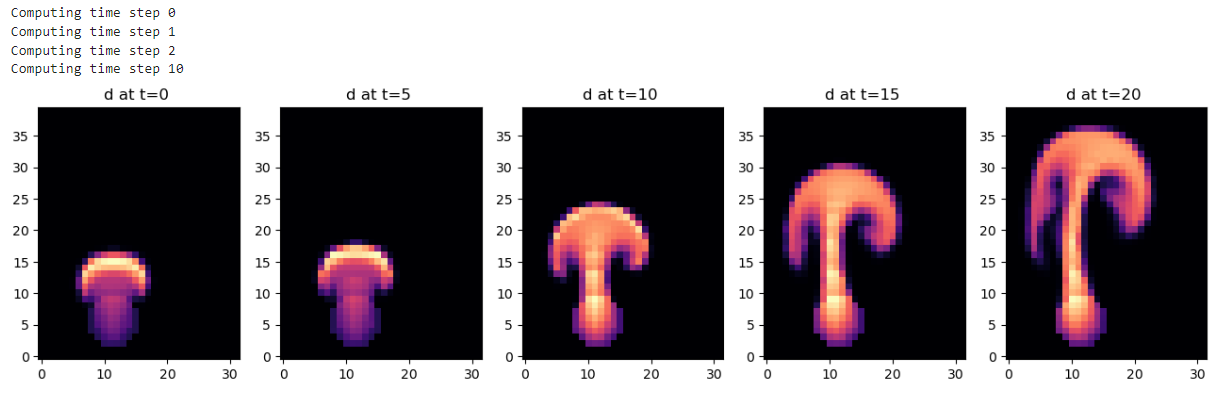
- 이전에 10번 반복한 상태를 다시 초기값으로 설정하고, 20번 더 반복한 결과
- 유입 지점이 왼쪽에 치우쳐진 상태로 시작했기 때문에, 점점 오른쪽으로 기울어지는 것을 볼 수 있음
u_x, u_t at each t
fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
axes[i].imshow(steps[i][1].numpy('y,x'), origin='lower', cmap='magma')
axes[i].set_title(f"u_x at t={ i*5} ")
fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
axes[i].imshow(steps[i][2].numpy('y,x'), origin='lower', cmap='magma')
axes[i].set_title(f"u_y at t={ i*5} ")
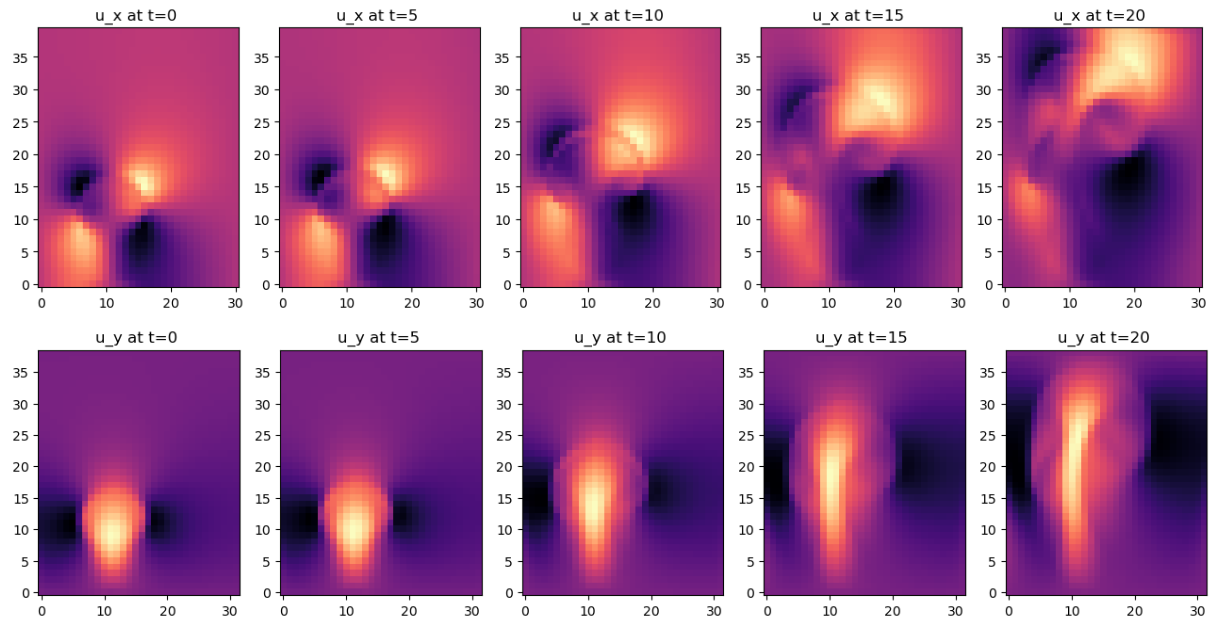
x, y 방향 속도의 변화를 각각 시각화한 결과
'논문' 카테고리의 다른 글
| [논문] ImageNet Classification with Deep Convolutional Neural Network (0) | 2024.03.25 |
|---|---|
| [논문] RGB-D camera pose estimation using deep neural network (0) | 2024.03.18 |
| [논문] Two-Level Attention-based Fusion Learning for RGB-D Face Recognition (0) | 2024.03.11 |
| [논문] A survey on RGB-D datasets (0) | 2024.03.10 |
| Physics-based Deep Learning - Introduction (0) | 2024.03.07 |