Welcome … — Physics-based Deep Learning
www.physicsbaseddeeplearning.org
Introduction

그림과 같이 양의 x축을 따라 있는 포물선에는 모든 점에 대해 두 가지 해결책이 있다.(주어진 x 값에 대해 두 개의 y 값(하나는 x축 위에, 다른 하나는 x축 아래에 있는)이 존재한다는 것)
Multimodal Target
- Mode 1 : 하나는 양의 y 값(하늘색 점으로 표시)
- Mode 2 : 다른 하나는 음의 y 값 (네이비색 점으로 표시)
Standard approach
- 전통적인 학습 방법으로 얻어진 결과
- 주의를 기울이지 않는다면, 가운데에 보이는 빨간색처럼 완전히 벗어난 근사값을 반환
Differentiable physics approach
- 물리학 기반의 다른 접근 방식을 사용하여 얻은 결과
- 이론적으로 녹색 선으로 표시된 모드 중 하나를 정확하게 나타낼 수 있음
1.1 Differentiable physics(DP)
미분가능한 물리학(Differentiable physics)이란 도메인 지식을 모델 방정식의 형태로 사용한 다음 이러한 모델의 이산화된 버전을 훈련 과정에 통합한다는 것을 의미한다. 미분 가능한 형식을 갖추는 것이 이 과정에서 매우 중요한데, 이는 신경망의 훈련을 지원하기 위함이다.
미분 가능한 형식을 갖추는 것이 이 과정에서 매우 중요한 이유?
→ Neural Network가 오류를 역전파하여 파라미터를 조정할 수 있도록 하기 위해서
→ 함수의 미분 가능성은 신경망이 데이터에서 패턴을 학습하고, 이상적인 함수 f∗에 대한 더 나 은 근사를 찾아나갈 수 있게 해준다.
DP를 통한 딥러닝의 특성 예제
함수 = 모델(Input → Output)
1. f∗ : X → Y
f*는 알려지지 않은 이상적인 목표 함수이다. 딥러닝의 목적은 이 이상적인 함수를 실제로 실현 가능한 형태, 즉 신경망 모델 f로 근사하는 것이다. 이 과정에서 이산화된 데이터 포인트를 사용하여 근사한다.
2. 𝒫: 𝑌 → 𝑍*
𝒫*는 우리가 원하는 어떤 실세계 행동을 인코딩하는 일반적인 미분 방정식이다. 이는 모델이 실세계의 물리적 속성을 반영하도록 하여, 그 속성을 만족하는 해결책들을 찾는 데 도움을 준다. ex) 시간에 따른 변화, 질량 보존
일반적으로 𝑓(모델)를 얻기 위해서는 데이터 수집 및 클래식한 지도 학습(supervised training)을 수행한다. 하지만 이 지도 학습 접근법과 대조적으로 미분 가능한 물리학 접근법(differentiable physics approach)을 사용하는 것은 물리 모델 𝒫의 이산화된 버전을 종종 사용함으로써 𝑓를 얻을 수 있다는 사실을 활용한다. 즉, 우리는 𝑓가 우리의 시뮬레이터 𝒫을 인지하고 그와 상호 작용하기를 원한다.
1.2 Finding the inverse function of a parabola
지도 학습과 미분 가능한 물리학(DP) 접근법의 차이를 보여주기 위한 실습 예제 부분
실습 예제
함수 𝒫 : 𝑦 → 𝑦^2가 주어졌을 때, [0, 1] 구간에서 𝑦에 대하여, 모든 𝑥에 대해 𝒫(𝑓(𝑥)) = 𝑥를 만족하는 알려지지 않은 함수 𝑓를 찾는 실습
흐름도
- 양의 제곱근과 음의 제곱근 중에서 무작위로 선택
- 네트워크, 손실, 그리고 훈련 구성을 정의
- ReLU 활성화 함수를 가진 세 개의 숨겨진 레이어를 가진 간단한 케라스(keras) 아키텍처 구현
- fit 함수를 사용하여 간단한 평균 제곱 오차 손실을 통한 훈련
- 시각화
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# X-Data
N = 200
X = np.random.random(N)
# Generation Y-Data
sign = (- np.ones((N,)))**np.random.randint(2,size=N)
Y = np.sqrt(X) * sign
# Neural network
act = tf.keras.layers.ReLU()
nn_sv = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, activation=act, input_shape=(1,)),
tf.keras.layers.Dense(10, activation=act),
tf.keras.layers.Dense(1,activation='linear')])
# Loss function
loss_sv = tf.keras.losses.MeanSquaredError()
optimizer_sv = tf.keras.optimizers.Adam(learning_rate=0.001)
nn_sv.compile(optimizer=optimizer_sv, loss=loss_sv)
# Training
results_sv = nn_sv.fit(X, Y, epochs=5, batch_size= 5, verbose=1)
# Results
plt.plot(X,Y,'.',label='Data points', color="lightgray")
plt.plot(X,nn_sv.predict(X),'.',label='Supervised', color="red")
plt.xlabel('y')
plt.ylabel('x')
plt.title('Standard approach')
plt.legend()
plt.show()
실습 결과
x축 양쪽의 데이터 포인트 사이에서 평균을 내므로 위의 문제에 대해 만족스러운 해결책과는 거리가 먼 결과를 얻게된다. 빨간색 점들은 회색으로 표시된 해결책의 두 모드 중 하나와 전혀 가깝지 않다. 이는 단 200개의 포인트로 상대적으로 거칠게 샘플링되었기 때문이다.

1.3 A differentiable physics approach
미분 가능한 물리학 접근법을 적용하여 𝑓를 찾아보는 예제, 훈련 과정에 우리의 이산화된 모델 𝒫을 직접 포함시킨다. (동일한 𝑥 위치를 그대로 유지하고, 이전과 같은 아키텍처를 신경망 인스턴스 nn dp를 사용)
주요 특징
- 손실함수가 핵심적이다. (손실에 함수 f를 직접 통합한다. 이 간단한 경우에서, 손실 dp 함수는 예측된 y의 제곱을 단순히 계산)
- 평균 제곱 오차 항 |𝑦_pred^2 − 𝑦_true^2|
- 유한차분 스텐실 평가, 솔버의 전체 암시적 시간-통합 단계를 계산으로 활용 가능
실습 코드
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# X-Data
N = 200
X = np.random.random(N)
# Generation Y-Data
sign = (- np.ones((N,)))**np.random.randint(2,size=N)
Y = np.sqrt(X) * sign
# Neural network
act = tf.keras.layers.ReLU()
# Model
nn_dp = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, activation=act, input_shape=(1,)),
tf.keras.layers.Dense(10, activation=act),
tf.keras.layers.Dense(1, activation='linear')])
#Loss
mse = tf.keras.losses.MeanSquaredError()
def loss_dp(y_true, y_pred):
return mse(y_true, y_pred ** 2)
optimizer_dp = tf.keras.optimizers.Adam(learning_rate=0.001)
nn_dp.compile(optimizer=optimizer_dp, loss=loss_dp)
#Training
results_dp = nn_dp.fit(X, X, epochs=5, batch_size=5, verbose=1)
# Results
plt.plot(X,Y,'.',label='Datapoints', color="lightgray")
#plt.plot(X,nn_sv.predict(X),'.',label='Supervised', color="red") # optional for comparison
plt.plot(X,nn_dp.predict(X),'.',label='Diff. Phys.', color="green")
plt.xlabel('x')
plt.ylabel('y')
plt.title('Differentiable physics approach')
plt.legend()
plt.show()
학습 결과
- 위 접근법에서는 네트워크가 현재 예측을 바탕으로 이산 모델을 평가하여, 사전에 계산된 해결책 대신, 네트워크의 예측 근처에서 가장 좋은 모드를 찾는다. 네트워크가 단순히 데이터 포인트들의 평균을 찾는 대신, 실제로 원하는 해결책에 더 근접한 값을 학습하게 해준다.
- 즉 , 네트워크가 해결책의 다양한 모드 중 하나를 선택하도록 하고, 두 모드 사이의 평균값을 예측하는 것을 피할 수 있게 한다. 그 결과, 신경망은 문제에 대한 더 정확하고 현실적인 해결책을 학습할 수 있다.
- 현재 신경망 구성은 단일 함수로 해결책을 모델링한다. 따라서 여러 모드를 표현하기에는 한계가 있기 때문에 여러 모드를 포착하기 위해 신경망을 확장하여 출력의 전체 분포를 포착하고 추가 차원으로 매개변수화해야 한다.
- 이 예시에서 𝑥가 0에 가까운 구간은 여전히 부정확하다. 네트워크는 여기서 본질적으로 포물선의 한쪽 반을 선형 근사한다. 이는 부분적으로 약한 신경망 때문이다.
1.4 Discussion
지도 학습에 대한 실패 사례로 특히, PDES(부분 적분 방정식)와 같은 문제에서는 가능한 해결책(모드)이 여러 개 존재하기 때문에 지도 학습을 사용하는 것은 더 위험하다. 만약 지도 학습을 이런 상황에 적용한다면, 학습된 모델이 단지 이러한 다양한 모드들의 '평균'을 내는 결과를 내놓을 수 있다. 이는 원하는 실제 해결책을 반영하지 못하며, 모델의 예측이 실제 문제에 적용할 때 정확하지 않을 수 있다.
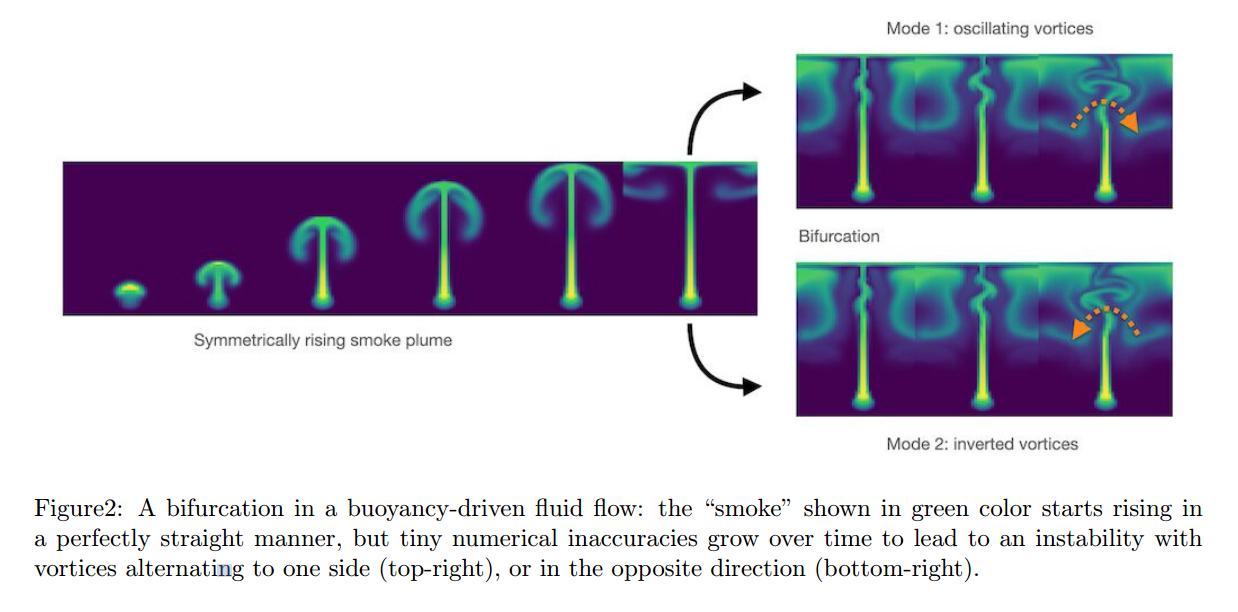
유체 흐름에서의 분기(Bifurcations)는 위 내용을 뒷받침하는 좋은 예제로, 처음에는 직선으로 올라가기 시작하지만, 그 움직임에 있는 미세한 교란으로 인해 임의의 방향으로 진동하기 시작한다. 만약 이런 경우 지도학습 같이 두 모드를 평균 내는 방식을 사용한다면, 위의 포물선 예제와 유사한 비물리적인, 직선적인 흐름이 나온다.
마찬가지로, 많은 수치 해결책에서 다양한 모드를 가지고 있으며, 일반적으로 이러한 모드들을 평균내는 것보다는 그것들을 복구하는 것이 중요하다.
1.5 Next steps
더 다양하고 복잡한 예제를 보여줄 예정
'논문' 카테고리의 다른 글
| [논문] RGB-D camera pose estimation using deep neural network (0) | 2024.03.18 |
|---|---|
| Physics-based Deep Learning - Overview (0) | 2024.03.15 |
| [논문] Two-Level Attention-based Fusion Learning for RGB-D Face Recognition (0) | 2024.03.11 |
| [논문] A survey on RGB-D datasets (0) | 2024.03.10 |
| [논문] U-Net: Convolutional Networks for Biomedical Image Segmentation (0) | 2024.03.03 |