반응형
1197번: 최소 스패닝 트리
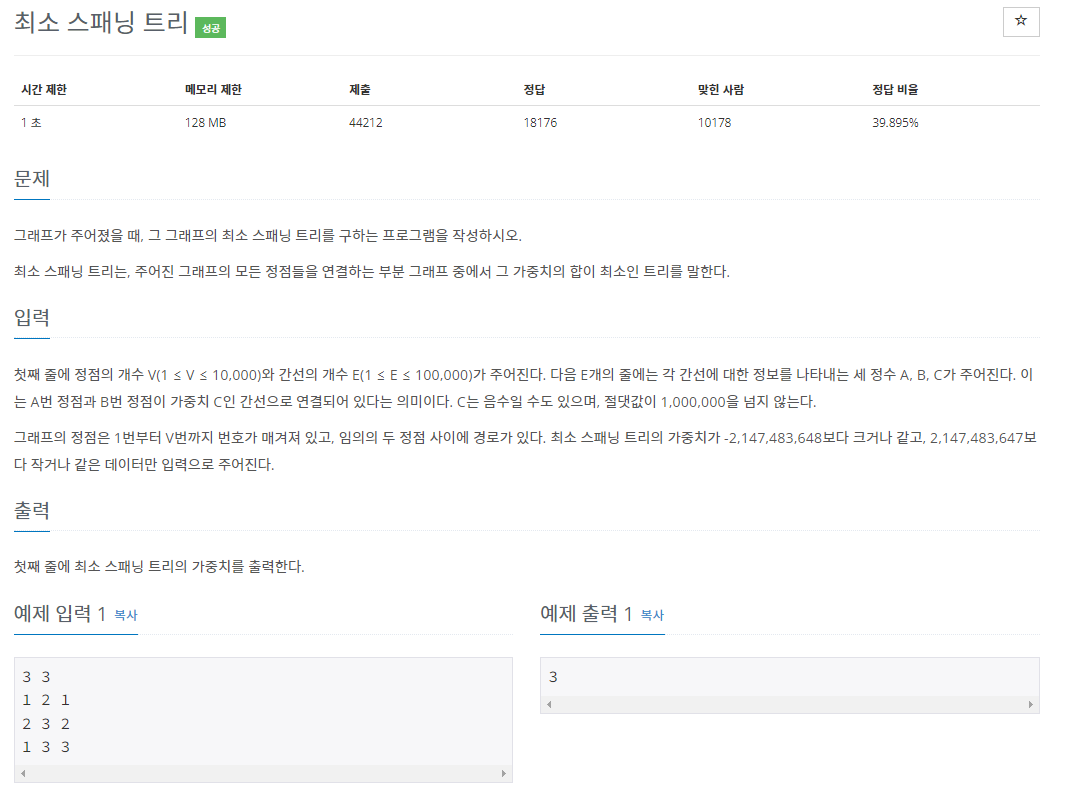
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이
www.acmicpc.net
알고리즘 분류
- 그래프 이론
- 최소 스패닝 트리
SOLUTION
import sys
# 크루스칼 알고리즘 사용하여 최소 가중치를 구한다
def find(parent, x):
if parent[x] != x:
parent[x] = find(parent, parent[x])
return parent[x]
def union(parent, A, B):
root_A = find(parent, A)
root_B = find(parent, B)
if root_A < root_B:
parent[root_B] = root_A
else:
parent[root_A] = root_B
V, E = map(int, sys.stdin.readline().split())
parent = [i for i in range(V+1)] # 부모 테이블 초기화
nodes = []
result = 0
for _ in range(E):
A, B, cost = map(int, sys.stdin.readline().split())
nodes.append((cost, A, B))
# cost가 작은 순으로 정렬
nodes.sort()
for i in range(E):
cost, A, B = nodes[i]
# find 함수 실행시, 부모노드가 다르면 union 함수 수행
if find(parent, A) != find(parent, B):
union(parent, A, B)
result += cost
print(result)'코딩테스트 대비 > 단계별 코딩 테스트 준비(27일 과정)' 카테고리의 다른 글
| [최소 신장 트리/Python] 17472번: 다리 만들기 2 - 효과는 굉장했다! (0) | 2022.02.19 |
|---|---|
| [트리/Python] 5639번: 이진 검색 트리 - 효과는 굉장했다! (0) | 2022.02.19 |
| [트리/Python] 2263번: 트리의 순회- 효과는 굉장했다! (0) | 2022.02.19 |
| [투 포인터/Python] 1806번: 부분합 - 효과는 굉장했다! (0) | 2022.02.19 |
| [투 포인터/Python] 3273번: 두 수의 합 - 효과는 굉장했다! (0) | 2022.02.19 |