반응형
Softeer
연습문제를 담을 Set을 선택해주세요. 취소 확인
softeer.ai
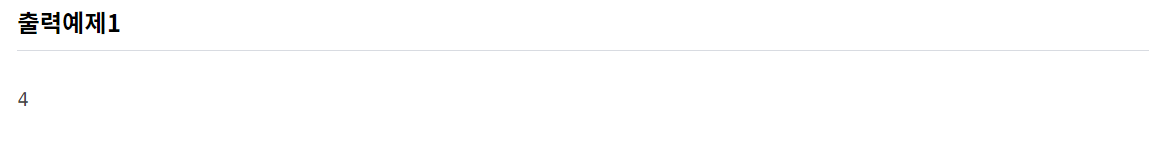
SOLUTION
import sys
import bisect # 이분 탐색
N = int(sys.stdin.readline())
stone_height = list(map(int, sys.stdin.readline().split()))
dp_front = [stone_height[0]] # 앞 쪽 기준 밟을 수 있는 돌의 유효한 오름차순 높이
dp_back = [stone_height[-1]] # 뒷 쪽 기준 밟을 수 있는 돌의 유효한 오름차순 높이
front_cnt = [1] * N # 앞에서 부터 밟은 돌의 갯수
back_cnt = [1] * N # 뒤에서 부터 밟은 돌의 갯수
# 앞 쪽 기준
for i in range(N):
if stone_height[i] > dp_front[-1]:
dp_front.append(stone_height[i])
else:
# 이분탐색을 이용하여 logN의 복잡도로 이전의 가장 큰 원소의 idx값을 찾는다.
idx = bisect.bisect_left(dp_front, stone_height[i])
dp_front[idx] = stone_height[i]
front_cnt[i] = len(dp_front)
# 뒷 쪽 기준
stone_height.reverse()
for i in range(N):
if stone_height[i] > dp_back[-1]:
dp_back.append(stone_height[i])
else:
# 이분탐색을 이용하여 logN의 복잡도로 이전의 가장 큰 원소의 idx값을 찾는다.
idx = bisect.bisect_left(dp_back, stone_height[i])
dp_back[idx] = stone_height[i]
back_cnt[N-i-1] = len(dp_back)
ans = 0
for i in range(N):
ans = max(ans, front_cnt[i] + back_cnt[i])
print(ans-1) # 가장 높은 크기의 돌이 2번 밟히기 때문에 -1 을 한다.
징검다리의 앞, 뒷 쪽을 기준으로 LIS(최장 증가 부분수열)을 각각 구하고, 이 중 두개의 합의 최대인 수에서 -1 을 뺀 값을 구한다. 이 때, -1 을 하는 이유는 가장 높은 크기의 돌은 2번 밟히기 때문이다.
N 의 범위가 3 × 10 ^ 5 이기 때문에, 이중 for문을 통해 가장 큰 이전의 Index값을 구하면 시간복잡도가 O(N^2)으로 시간초과가 난다. 이를 해결하기 위해 이분탐색을 이용해 O(NlogN)의 복잡도로 시간초과가 나지 않고 문제를 풀 수 있다.
'코딩테스트 대비 > Softeer' 카테고리의 다른 글
| [Softeer/Python] 복잡한 조립라인2 ★★★★★ - 효과는 굉장했다! (0) | 2022.08.05 |
|---|---|
| [Softeer/Python] 복잡한 조립라인1 ★★★★☆ - 효과는 굉장했다! (0) | 2022.08.03 |
| [Softeer/Python] [인증평가(1차) 기출] 로봇이 지나간 경로 ★★★☆☆ - 효과는 굉장했다! (0) | 2022.07.24 |
| [Softeer/Python] 수퍼바이러스 ★★★☆☆ - 효과는 굉장했다! (0) | 2021.11.26 |
| [Softeer/Python] GINI야 도와줘 ★★★☆☆ - 효과는 굉장했다! (0) | 2021.11.25 |