반응형
14938번: 서강그라운드
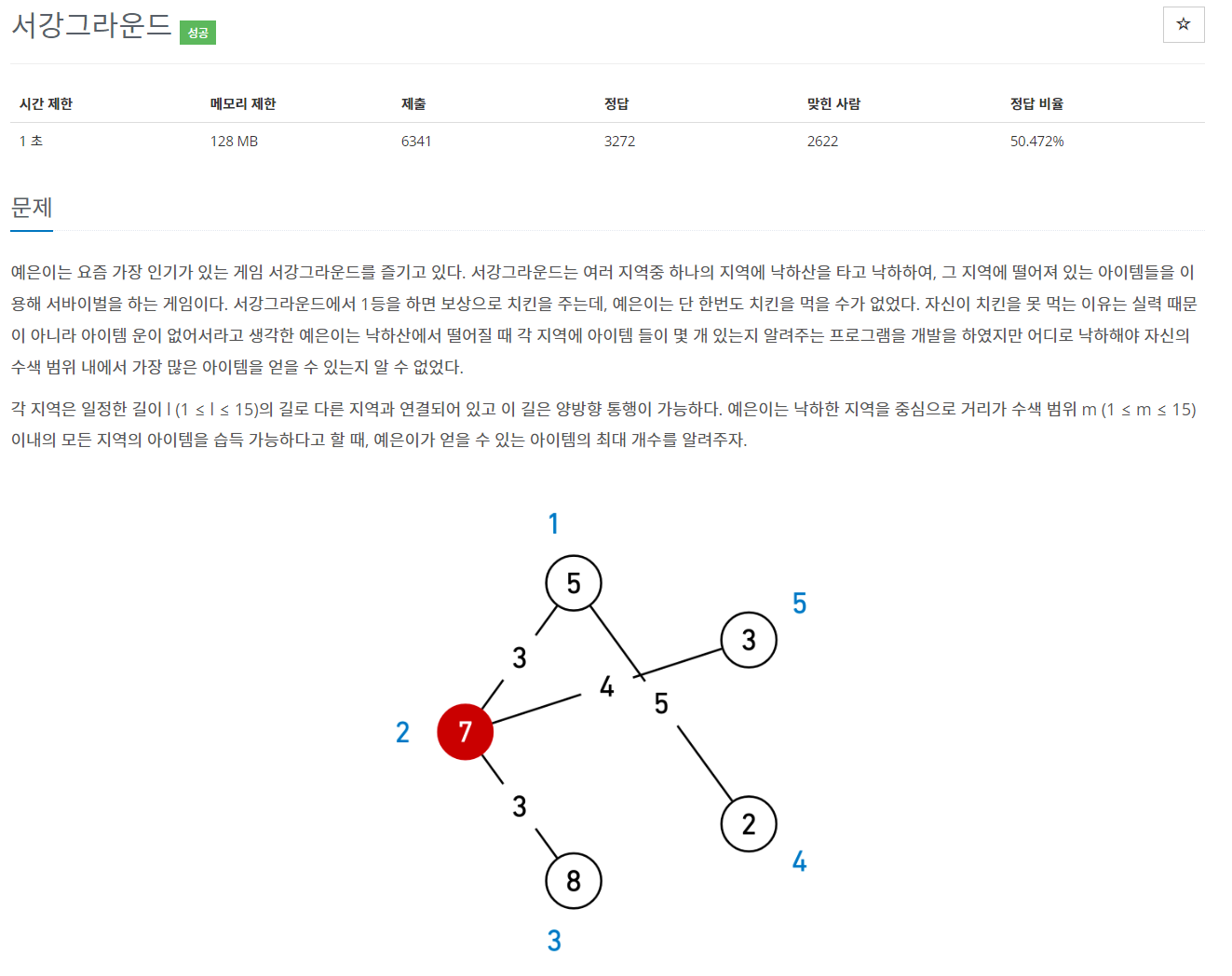
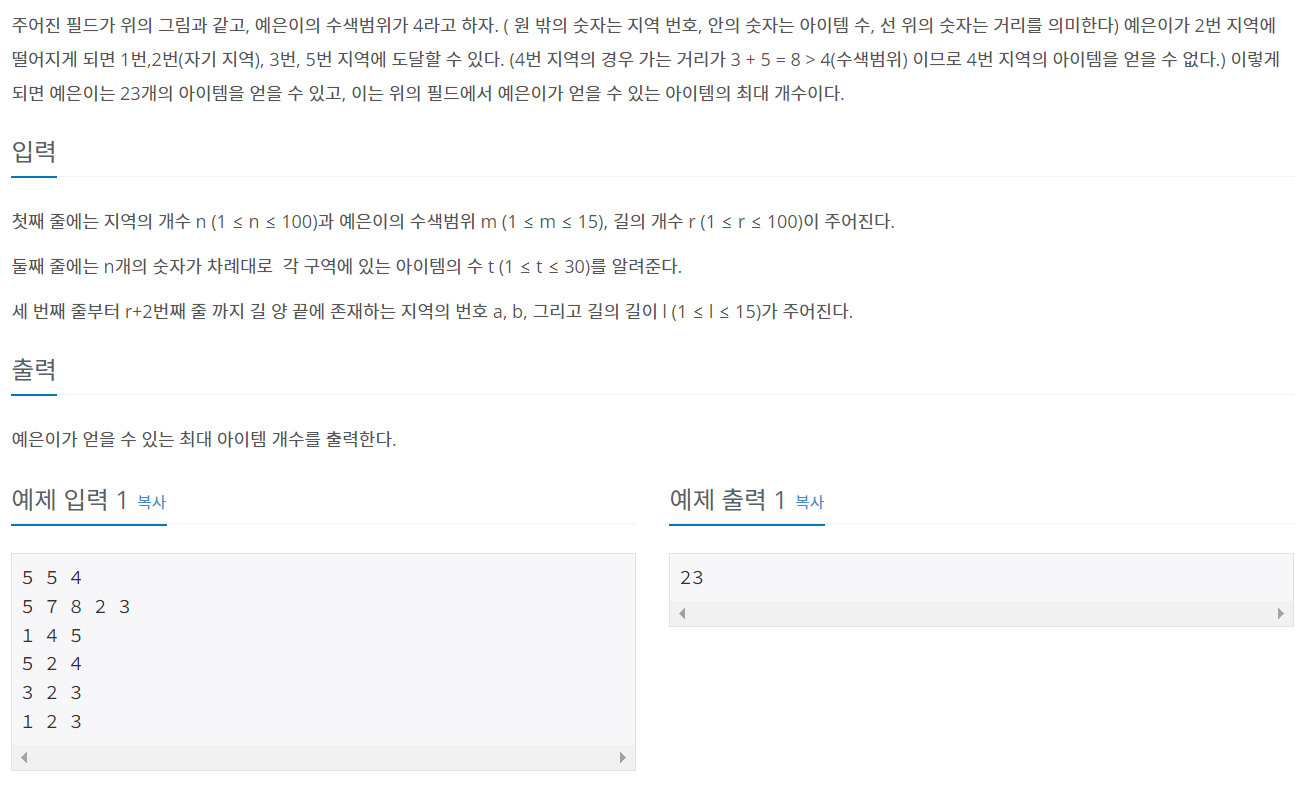
예은이는 요즘 가장 인기가 있는 게임 서강그라운드를 즐기고 있다. 서강그라운드는 여러 지역중 하나의 지역에 낙하산을 타고 낙하하여, 그 지역에 떨어져 있는 아이템들을 이용해 서바이벌을
www.acmicpc.net
알고리즘 분류
- 그래프 이론
- 데이크스트라
- 플로이드–워셜
SOLUTION
- Dijkstra O(NlogN)
import sys
import heapq
INF = sys.maxsize
def dijkstar(start):
heap = []
distance = [INF] * (n+1)
heapq.heappush(heap, (0, start))
distance[start] = 0
while heap:
wei, now = heapq.heappop(heap)
if distance[now] < wei:
continue
for next_node, w in graph[now]:
next_cost = wei + w
if next_cost < distance[next_node]:
distance[next_node] = next_cost
heapq.heappush(heap, (next_cost, next_node))
return distance
n, m, r = map(int, sys.stdin.readline().split())
items = list(map(int, sys.stdin.readline().split()))
graph = [[] * n for _ in range(n)]
for _ in range(r):
a, b, l = map(int, sys.stdin.readline().split())
graph[a-1].append((b-1, l))
graph[b-1].append((a-1, l))
ans = 0
for i in range(n):
tmp = 0
result = dijkstar(i)
for j in range(n):
if result[j] <= m:
tmp += items[j]
ans = max(ans, tmp)
print(ans)
- Floyd Warshall O(N^3)
import sys
INF = sys.maxsize
n, m, r = map(int, sys.stdin.readline().split())
items = list(map(int, sys.stdin.readline().split()))
graph = [[INF] * n for _ in range(n)]
print(graph)
for _ in range(r):
a, b, l = map(int, sys.stdin.readline().split())
graph[a-1][b-1] = graph[b-1][a-1] = l
for k in range(n): # 경유지
for i in range(n): # 시작점
for j in range(n): # 끝점
if i == j:
graph[i][j] = 0
else:
graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
ans = 0
for i in range(n):
tmp = 0
for j in range(n):
if graph[i][j] <= m:
tmp += items[j]
ans = max(ans, tmp)
print(ans)'코딩테스트 대비 > BOJ' 카테고리의 다른 글
| [Baekjoon/Python] 21736번 : 헌내기는 친구가 필요해 - 효과는 굉장했다! (0) | 2023.10.22 |
|---|---|
| [Baekjoon/Python] 17144번: 미세먼지 안녕! - 효과는 굉장했다! (0) | 2022.07.24 |
| [Baekjoon/Python] 14502번: 연구소 - 효과는 굉장했다! (0) | 2022.07.24 |
| [Baekjoon/Python] 13172번: Σ - 효과는 굉장했다! (0) | 2022.07.24 |
| [Baekjoon/Python] 12851번: 숨바꼭질 2- 효과는 굉장했다! (0) | 2022.07.24 |